 |
|||||
|---|---|---|---|---|---|
 |
Theories of the Aether
Articles relating to the Emergence | ||||
On the distribution of the planets Web Publication by Mountain Man Graphics,
Australia - Southern Winter 2004
 | |||||
 |
|||||
|---|---|---|---|---|---|
 |
Theories of the Aether
Articles relating to the Emergence | ||||
On the distribution of the planets Web Publication by Mountain Man Graphics,
Australia - Southern Winter 2004
 | |||||

Introduction |
|---|
This study of Maurice Allais contains 69 pages and is finished with a bibliography naming 29 different research works dating from 1766 to our present days. It has not been yet the object of a publication. Here follow a resume of his paper. The distances of the sun to the planets of the solar system and the distances of the planet central of the satellites of Jupiter, Saturn and Uranus are not just any numbers. We observe that those distances answer to a mathematical law, yet not knowing as of today of an explicit reason. 1. Anterior Works. The effort to bring to attention the relation of the proportional distances of and in the solar system as very ancient origin and Wolf, the German Astronomer has been one of the first to realize the importance of those researches in 1741. Titius, rediscovered it in 1766. Yet it is mainly known due to Bode who published his work in 1772. It is known as the Titius- Bode law. Subsequently numerous contribution have been presented, some of greater value than others. To the fore ranks of those contributions, we can situate the formulation of Gaussin, simultaneously valuable for the planets and for the satellites of the planets. 2. Contribution of Maurice Allais. The research work of Maurice Allais inscribes itself in the long lineage of all those publications. His formulation depends only on 2 parameters and situates itself in the way opened by Gauss in 1880. The formula is written as: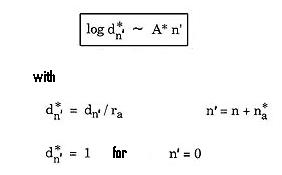
Where: dn’ represents the distance of the satellite to the central planet, and ra the radius of the central planet, and na* a positive integer. The parameter A* and na*, represent 2 parameter of adjustment. The values of the n represent the numerical order of the satellite to the central planet. Altogether this formulation gives excellent results for the system of the Sun, of Jupiter and of Saturn and Uranus. The estimations of the dn, ra results of the relation of the Celestial mechanics, which place itself in the isotropic and Euclidian space. The considered formulation can be interpreted as corresponding to a localization of the planets and of the satellites of the planets at the sinusoids knots of the period T=2 in the space of the n’. As of today, no theoretical explanation has been given for this formulation, which brings the intervention of the neperien logarithms of the distance in space fundamentally isotrope and Euclidian of the celestial mechanic. Nevertheless, it certainly doesn’t diminish its importance and significance.Author: Maurice Allais (22-DEC-2003)
Translator: François Bocquet 01-AUG-2004
