 |
|||||||
|---|---|---|---|---|---|---|---|

| Selected Book ReviewsOrder Out of Chaos | ||||||
Web Publication by Mountain Man Graphics, Australia


 |
|||||||
|---|---|---|---|---|---|---|---|

| Selected Book ReviewsOrder Out of Chaos | ||||||

Introduction |
|---|
In the exposition of one of the main thematic threads of their subject matter, the authors itemise three types of conceptually different systems, only two of which were academically studied and (generally) understood by the progressive expansion of scientific research and theory in relation to the study of natural phenomena exhibited around us - in our terrestrial environment upon this earth, and in the local cosmic environment within which the terrestrial is embedded.
Systems which are in equilibrium or systems which are close to equilibrium are the first two phenomena presented, during which it is noted that such systems are - almost exclusively - the subject matter of the traditional and classical sciences. Such systems are relatively stable, exhibiting known and predictable characteristics which may be represented in parameter driven mathematical models.
However Prigogine chose to attempt investigation of a third and largely ignored class of systems - those which were far from equilibrium. His research earned him the Nobel Prize in 1977, for his work on the thermodynamics of nonequlibrium systems, and his contribution towards the understanding of natural processes and their descriptions has earnt him the respect of many scientists and academics in many fields. The authors have subtitled their publication Man's New Discourse with Nature, and progressively introduce and discuss the conceptual differences between the traditional mechanistic interpretation of the so-called laws of cause and effect and the inability of this paradigm alone to provide explanation for that class of phenomenal systems in which equilibrium conditions are not maintained.
The following selected passages below represent quotations from the authors which - when reading the book - I collected for my own archive of research material. If it becomes useful and a resource to other students of life, then the small time spent in preparing it for the net will have been well spent.
All the best,
Pete Brown
Mountain Man Graphics,
Newport Beach, Australia
Southern Winter of 1997
E-Mail: prfbrown@magna.com.au
Far from Equilibrium Systems |
|---|
Whenever we define potential, we are defining a stable world in which the systems follow an evolution that leads them to a static situation that is established once and for all.
When the thermodynamic forces acting on a system become such that the linear region is exceeded, however, the stability of the stationary state, or its independence from fluctuations, can no longer be taken for granted. Stability is no longer the consequence of the general laws of physics. We must examine the way a stationary state reacts to the different types of fluctuations produced by the system or its environment. In some cases, the analysis leads to the conclusion that a state is "unstable" - in such a state, certain fluctuations, instead of regressing, may be amplified and invade the entire system, compelling it to evolve toward a new regime that may be qualitatively quite different from the stationary states corresponding to minimum entropy production.
[Page 140]
The Nature of Turbulence |
|---|
The clinamen, this spontaneous, unpredictable deviation, has often been criticised as one of the main weaknesses of Lucretian physics, as being something introduced adhoc. In fact, the contrary is true - the clinamen attempts to explain events such as laminar flow ceasing to be stable and spontaneously turning into turbulent flow. Today hydrodynamic experts test the stability of fluid flow by introducing a perturbation that expresses the effect of molecular disorder added to the average flow. We are not so far from the clinamen of Lucretius!
Fo a long time turbulence was identified with disorder or noise. Today we know that this is not the case. Indeed, while turbulent motion appears as irregular or chaotic on the macroscopic scale, it is, on the contrary, highly organised in the microscopic scale. The multiple space and time scales involved in turbulence correspond to the coherent behaviour of millions and millions of molecules. Viewed in this way, the transition from laminar flow to turbulence is a process of self-organisation. Part of the energy of the system, which in laminar flow was in the thermal motion of the molecules, is being transferred to macroscopic organised motion.
[Page 141]
Dissipative Structures |
|---|
Classical thermodynamics leads to the concept of "equilibrium structures" such as crystals. Benard cells are structures too, but of a quite different nature. That is why we have introduced the notion of "dissipative structures", to emphasise the close association, at first paradoxical, in such situations between structure and order on the one side, and dissipation or waste on the other. Heat transfer was consdered a source of waste in classical thermodynamics. In the Benard cell it becomes a source of order.
The interaction of a system with the outside world, its embedding in nonequilibrium conditions, may become in this way the starting point for the formation of new dynamic states of matter - dissipative structures. Dissipative structures actually correspond to a form of supramolecular organisation.
Page 143
Encounter with Molecular Biology |
|---|
Although the effects of nonlinear reactions (the presence of the reaction product) have a feedback action on their "cause" and are comparitively rare in the inorganic world, molecular biology has discovered that they are virtually the rule as far as living systems are concerned. Autocatalysis (the presence of X accelerates its own synthesis), autoinhibition (the presence of X blocks a catalysis needed to synthesise it), and crosscatalysis (two products belonging to two different reaction chains activate each other's synthesis) provide the classical regulation mechanism guaranteeing the coherence of the matabolic function.
[...]
Biological systems have a past. Their constuitive molecules are the result of an evolution; they have been selected to take part in the autocatalytic mechanisms to generate very specific forms of organisation processes.
Page 153
Nonequilibrium systems and gravitation |
|---|
Gravitation obviously will modify the diffusion flow in a reaction diffusion equation. Detailed calculations show that this can be quite dramatic near a bifurcation point of an unperturbed system. In particular, we can conclude that very small gravitational fields can lead to pattern selection.
Page 163
From Euclid to Aristotle |
|---|
It has often been said - and we have already repeated it - that modern science was born when Aristotelian space, for which one source of inspiration was the organization and solidarity of biological functions, was replaced by the homogeneous and isotropic space of Euclid. However, the theory of dissipative structures moves us closer to Aristotle's conception. Whether we are dealing with a chemical clock, concentration waves, or the inhomogeneous distribution of chemical products, instability has the effect of breaking symmetry, both temporal and spatial. In a limit cycle, no two instants are equivalent; the chemical reaction acquires a phase similar to that characterizing a light wave, for example. Again, when a favored direction results from an instability, space ceases to be isotropic. We move from Euclidian to Aristotelian space!
It is tempting to speculate that the breaking of space and time symmetry plays an important part in the fascinating phenomena of morphogenesis. These phenomena have often led to the conviction that some internal purpose must be involved, a plan realized by the embryo when its growth is complete. At the beginning of this century, German embryologist Hans Driesch believed that some immaterial "entelechy" was responsible for the embryo's development. He had discovered that the embryo at an early stage was capable of withstanding the severest perturbations and, in spite of them, of developing into a normal, functional organism. On the other hand, when we observe embryological development on film, we "see" jumps corresponding to radical reorganizations followed by periods of more "pacific" quantitative growth. There are, fortunately, few mistakes. The jumps are performed in a reproducible fashion. We might speculate that the basic mechanism of evolution is based on the play between bifurcations as mechanisms of exploration and the selection of chemical interactions stabilising a particular trajectory.
Page 171
ReEnchantment of Nature |
|---|
We may summarise the situation as we see it today in the following diagram:
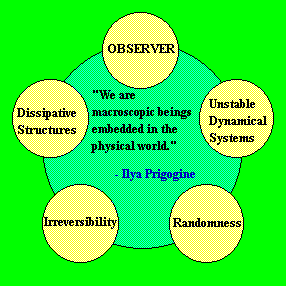 |
The Dynamic | |
|---|---|---|
Pages 299 - 300
Other Resource Links |
|---|
Related Usenet Post ... |
|---|
> Could anyone tell me in layman terms what he discovered? Apparently he's
> come up with a way to combine statistical and Newtonian physics, so that
> irreversible systems now can be reversed (ie friction and time's arrow)
In sci.astro, agraps@netcom.com (Amara Graps) responds as follows:
Prigogine won the Nobel Prize in 1977 for his work in the thermodynamics of nonequilibrium systems.
Prigogine is primarily a chemist. He was well established in his field 20 years ago, so what he's done since then, is branch out into related areas. As I understand it, his main discovery has been the discovery of "chemical clocks." These are chemical reactions that oscillate in a very regular and precise way. Prigogine predicted that they should exist from a theoretical chemistry standpoint several decades ago. In the late 1950's, one of his research group came back from a visit with a colleague in Russia, announcing that they had a chemical reaction that did just what Prigogine predicted. The reaction is now known as the Belousov-Zhabotininskii reaction and it is the oxidation of citric acid by potassium bromate catalyzed by the ceric-cerous ion couple.
To Prigogine, irreversibility is a fundamental property of physics. Prigogine proposes that entropy production is part of an operator (operators map functions onto functions), and time is an operator. And that the time that we are all familiar with from classical mechanics is just an ensemble average of this operator with a state vector. I.e. "ordinary" time is an average over his new time operator. And that "age" is DEpendent of the distibution.
So what does that mean about operators..? Let's say that we wish to know the time evolution of a system. In both quantum mechanics and classical mechanics, the Hamiltonian operator determines how the system will evolve in time. The evolution that we are all familiar with is a reversible and deterministic evolution (We can say that the reversible change of a wave function that represents the quantum system corresponds to a reversible motion along a trajectory that represents the classical system.) The wave function or trajectory represents the maximum knowledge of the system.
Prigogine has incorporated reversible and irreversible parts into a new microscopic equation/description. The equation contains an operator analogous to the Hamiltonian, that is a new "time evolution operator" that now can drive the system to both equilibrium or nonequilibrium states. Entropy is produced by the even part of the new time evolution operator and he has defined an operator for that.
An example that Prigogine gives looks at the conventional and his unconventional determination of energy levels in a quantum system. In the conventional quantum mechanics, both the energy levels and the time evolution of them are determined by the same quantity: the Hamiltonian operator. Prigogine's method allows him to use two different operators: the time operator for time evolution and another operator (a "superoperator" that can act on other operators) to determine the energy levels. So in this way, instead of having the "particle" and the "interaction" (conventional view), we have the physical _process_ that contains electrons, photons, etc. that drive the total system. This process is "real" and cannot be "transformed" away by any change of representation.
Or another way to look at it: the classical order says particles come first and the Second Law of Thermodynamics comes later, while Prigogine says that we must first introduce the Second Law before being able to define the entities.
Another one of Prigigine's main themes is that nonlinear interactions frequently lead to order (which he calls "dissipative structures") through fluctuations. A dissipative structure is order visible on a macroscale which can exchange energy with the outside world. In particular, if the system is in a far-from-equilibrium-state this can happen.
In fact, in Prigogine's view, we can now recognize ourselves as a kind of evolved form of dissipative structure, and we can justify, in an objective way, the distinction between the future and the past. How? The time symmetry is broken in the following way: the existence of irreversible processes on the microscopic level through kinetic equations violates the symmetry of the canonical equations. And dissipative structures may, in turn, break the symmetries of space-time.
I don't know if I managed to put this in layman's terms. His theory is very mathematical. But I think this is cool stuff.
You can find out more about Prigogine's ideas in the books: Order Out of Chaos (few or no equations) and From Being to Becoming (very technical, but the same subject matter).
Amara
E-Mail: agraps@netcom.com
WWW: http://www.amara.com/